
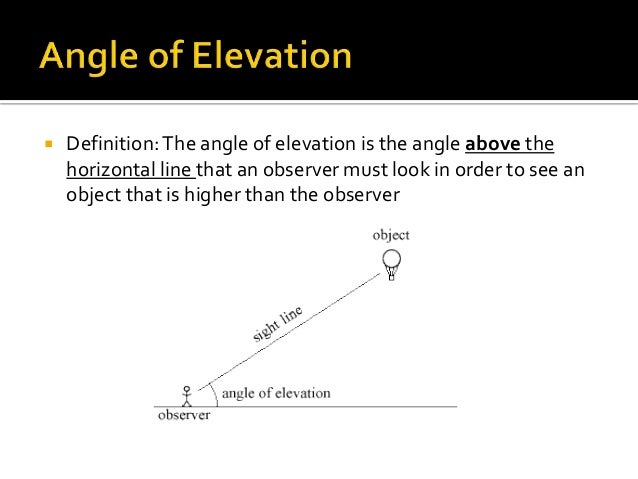
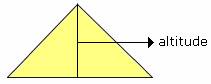
The orthic triangle is also homothetic to two important triangles: the triangle formed by the tangents to the circumcircle of the original triangle at the vertices (the tangential triangle), and the triangle formed by extending the altitudes to hit the circumcircle of the original triangle. What is an example of altitude in geometry An altitude is a line segment in a triangle from a vertex and perpendicular to the opposite side, it is also known as the height of a triangle. This circle is better known as the nine point circle of a triangle. The circumcircle of the orthic triangle contains the midpoints of the sides of the original triangle, as well as the points halfway from the vertices to the orthocenter. The next easiest to find is the one from B B B to A C AC A C, since A C AC A C can be calculated as y = 12 5 x y=\frac n m for relatively prime positive integers m m m and n n n. The easiest altitude to find is the one from C C C to A B AB A B, since that is simply the line x = 5 x=5 x = 5. What are the coordinates of the orthocenter? This is especially useful when using coordinate geometry since the calculations are dramatically simplified by the need to find only two equations of lines (and their intersection). Finally, if the triangle is right, the orthocenter will be the vertex at the right angle.īecause the three altitudes always intersect at a single point (proof in a later section), the orthocenter can be found by determining the intersection of any two of them. If the triangle is obtuse, the orthocenter will lie outside of it. If the triangle is acute, the orthocenter will lie within it. The location of the orthocenter depends on the type of triangle.


 0 kommentar(er)
0 kommentar(er)
